The era we are in is advocating "the bigger the better." In a recent SynAudCon forum post, I said that this reason may not apply to the length of the FIR filter.
When this article is written, the length of the filter supported by the DSP is usually 1024 tabs, and some are up to 4096 points. Why don't I want or need a longer FIR filter? If the manufacturer introduces a 8192-point FIR filter in the DSP, will I abandon the competitive product and choose it?
The lower the frequency, the longer the time
First, we need a document for practice and experimentation. The measurement data of the speakers can be used, but a slightly simpler file is easier to help us find important points.
Please see Figure 1 for reference. I created this series of boost filters (separated symmetric equalizers with an octave bandwidth) in the FIRCapture software and saved them as WAV files. This response can be easily created with any 9-band parametric equalizer.
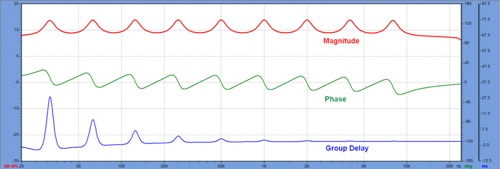
Figure 1: Conversion function of the author test file (created by FIRCapture software)
I chose Q=6 to maximize the overlap between filters. This set of filters constitutes a filter that is identical to the response of the loudspeaker, not to mention the high-pass and low-pass responses that are essential at the highest and lowest frequencies. If this is the response of a speaker (let's assume this), we will want to equalize the raised portion to get a flatter overall response. Through this document, we can well investigate the frequency resolution of the FIR filter.
The frequency domain view shows the amplitude, phase, and group delay of the frequency response. Note that phase and group delay are two different ways to show how the filter changes its time behavior as the signal passes. Since the phases are relative, the phase behavior of each bump is the same.
In the previous article I demonstrated that the minimum phase response of a bandpass filter is first positive, then returns to the origin at the center frequency of the filter, and finally to the negative. This phase offset will cause a frequency dependent ringing phenomenon (Ringing) to be generated by the signal of the filter. The duration of the ringing phenomenon is indicated by the group delay map.
Figure 2 is a detailed frequency/time domain map of the filter. Figure 3 shows the wavelength of the center frequency of each separation octave. What is the relationship between the two? Since the speed of sound is about 1 foot per millisecond (ft/ms), the center frequency of each octave is approximately equal to the time required for one cycle. The concept of wavelengths shows that sound waves are related to time and space in a very imaginative way, as is the response of the filter.
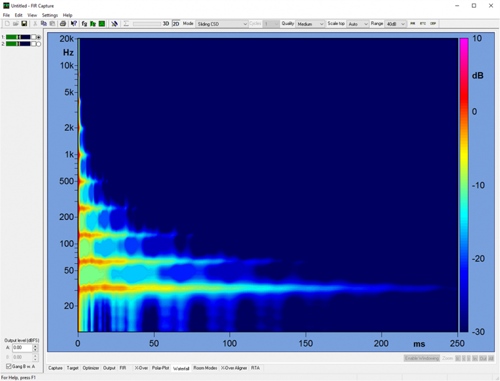
Figure 2: Frequency domain vs. time domain plot of the same signal. Note that in the time domain view, the filter's ringing phenomenon (non-delay) is raised. Also note that the resolution of the ringing phenomenon is better in this view (red is approximately equivalent to the group delay icon)
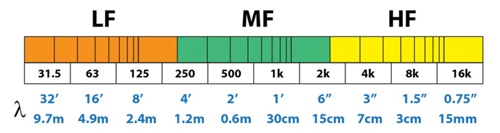
Figure 3: Wavelength of each octave center frequency. Regardless of the type of filter used, the time/frequency/wavelength relationship ultimately determines the resolution group delay (GD) required for the FIR filter to be proportional to the frequency wavelength of the filter. The lower the frequency, the group delay. The longer it is. From the name alone, it seems to refer to the delay caused by the signal passing through the filter, which is a bit misleading. The storage properties of the filter cause ringing, which adds extra cycles to the signal.
The group delay shows how long the boost filter takes up. It is not surprising that the low frequency bulge has a long ringing. The group delay is inversely proportional to the filter frequency (proportional to the wavelength). When the phase offset is equal, the lower the frequency, the longer the group delay.
For the convenience of demonstration, we take the signal processing link shown in Figure 4 as an example. We enter a test signal to see what happens. Figure 5 shows the results of a 2-channel oscilloscope display. The blue trajectory is a 1000 Hz 6.5-cycle wavelet. This is one of the Don Keele test signals. The red trace is the result of this signal passing through a 1000 Hz boost filter. Note that the original signal and the signal processed by the filter are in phase, but the signal period through the filter is increased. This is the ringing phenomenon observed in the time domain. A ringing phenomenon that reduces the filter will take the same amount of time.
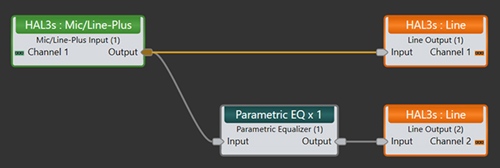
Figure 4: Signal processing settings on the Rane HAL DSP for the ringing of the delay filter.
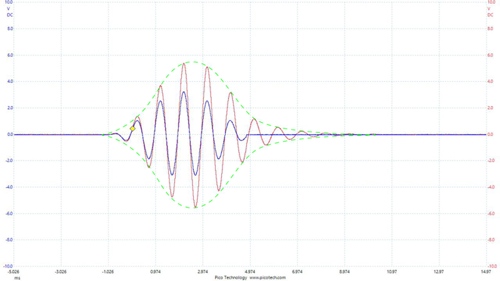
Figure 5: A 6.5-cycle (1 kHz) wavelet. The blue curve is the original signal. The red curve is the response of the signal after passing through a 1 kHz 6dB boost filter (Q=6). Note that the signal passing through the filter module itself does not cause a delay, but the signal envelope (green outline) spans longer.
IIR equalization
How does an analog or digital wireless impulse response filter (IIR filter) correct the response? It must be to produce an amplitude response and phase offset opposite to the bump. Since the IIR filter is cyclic, a portion of the output signal is returned to the input for reprocessing using feedback (can charge and discharge analog capacitors).
Therefore, the IIR filter has no low frequency limit during operation (at least when compared to the FIR filter) and does not cause a large amount of processing delay. As long as there is an input signal, there will be an output signal, and the impulse response of the filter (theoretically) will never decay to zero.
The forward group delay is a sign of the narrowband boost filter (Figure 1), while the negative group delay is the sign of the cut filter. Figure 7 shows a set of IIR filters implemented by an EQ module of a popular DSP. By comparing the amplitude and phase of each of the bumps of Figure 1 with each notch of Figure 7, it can be seen that the equalizer of Figure 7 can fully correct the response of my file.
Incidentally, the group delay of the narrow-band signal does not represent the signal delay, but shows the duration of the filter ringing phenomenon. Some terms in audio are not literal, such as "Constant voltage," but this is another topic, so I won't go into details here.
Minimum phase FIR EQ
Let us discuss the minimum phase FIR. Its response can be exactly the same as the IIR filter generated by the parametric equalizer. The key difference is that the response of the FIR filter is completely independent of the drive signal. It is a finite length impulse response and frequency resolution is related to length.
Since T = 1/F, the lower the frequency to be affected, the longer the required filter length (time span, more points). Correcting the low frequency bumps requires introducing a conjugate of amplitude and phase at each frequency, which is also conjugated to the group delay. For low frequency bumps, this is a very long time span.
Look back at Figure 1. Since the filter is a minimum phase filter, the processing delay is small, similar to that of the IIR filter. The difference is that the bandwidth of the FIR filter is determined by its length (Figure 6), so a very long filter is needed to equalize the low frequency bumps. This is independent of the processing algorithm used to create the filter.
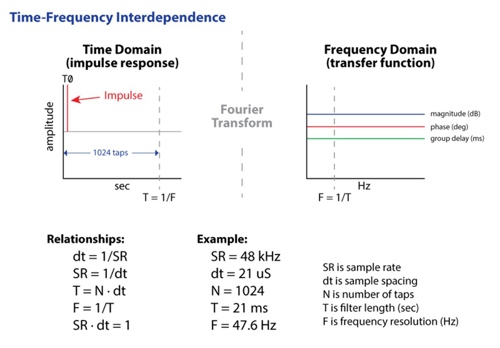
Figure 6: Correlation of time and frequency resolution. The frequency domain view takes the time of arrival of the pulse fact as a reference (T0) and the time span extends to T. Since a perfect pulse is reached at this time, this FIR is a pure delay, and its bandwidth is determined by the number of points.
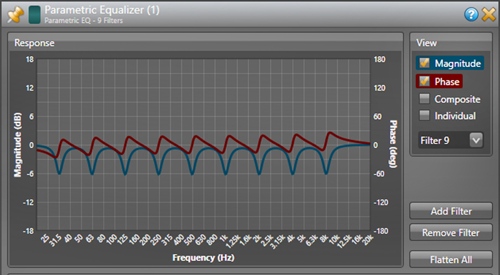
Figure 7: A parametric EQ module (IIR) can completely correct my model file. Its frequency resolution is higher than the FIR filter, and the DSP resources that need to be called are much less.
Frequency resolution
As can be seen from Figure 6, a 1024-point, minimum phase FIR filter with a sampling rate of 48 kHz has a length of 21 milliseconds. Since T = 1/F, the frequency resolution of this filter is 47.6 Hz.
What does this mean? This means the spacing between each data point in the frequency domain view.
It also represents the lowest frequency that the filter can affect. In fact, the frequency resolution is lower (the lowest frequency that can be affected is slightly higher), because it takes a few cycles to determine a certain frequency.
What if you add more points? Doubling the filter length will double the frequency resolution so that the frequency spacing between the data points becomes 24 Hz.
It also makes the low frequency limit to dive half, going to 24Hz. This trend will continue, with each doubling of the number of dots, which will cause the filter's response to dive by an octave. Therefore, a longer length FIR filter will make:
1) The filter is extended to a lower frequency.
2) The frequency response of the filter presents more detail because the data points are more dense.
In the case of a minimum phase FIR filter, more points are of great benefit because this means that the filter can be extended to lower frequencies. Since this is the minimum phase filter, there is no additional processing delay compared to the IIR filter. To get a smooth response to my sample file, it takes about 4096 points, which far exceeds the number of points that the existing DSP can support, which makes the debate that requires more bits more intensified.
Don't worry about the conclusion
Let us seriously consider it. The minimum phase FIR behaves like the minimum phase IIR filter, but requires enough points to affect the lowest frequency to be reached. Low frequency equalization requires a longer filter length.
But why create a minimum phase filter in the DSP through a FIR filter module that consumes a lot of system resources? A well-tuned parametric equalization module (IIR) will take up much less system resources, but produce the same smooth response with better frequency resolution (Figure 7). Using the least possible system resources to get the desired results is a best practice in the audio industry, and using FIR filters for minimum phase equalization is not efficient.
Let us then consider the case where the corrected response is not the minimum phase. In the reference, I added a second-order all-pass filter (500 Hz) to the response (Figure 8). This will cause a phase shift across the entire bandwidth of the filter, but with minimal impact on the amplitude response. In factual applications, this all-pass behavior may result from the use of a crossover network. The minimum phase FIR filter cannot compensate for such additional phase offsets.
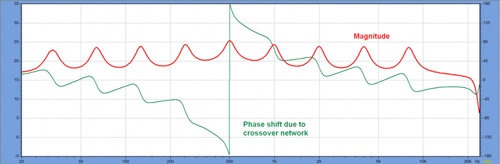
Figure 8: An all-pass filter has been added to the reference file. A non-minimum phase filter is finally formed. A linear FIR filter is required to correct this response.
Linear phase FIR
A linear phase FIR has a symmetric impulse response with the main signal arrival time in the middle of the impulse response (IR) (Figure 9). We set the arrival peak to a relative time zero, before which the time span provides a "negative time" arrival for the energy arrival after the conjugate main arrival peak.
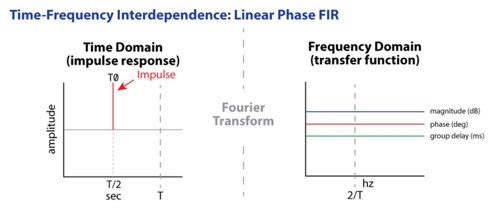
Figure 9: The linear phase filter stores up to half of the bits for phase equalization/echo cancellation and reduces the bandwidth of the filter by one octave. The above frequency domain view is referenced to the time (T0) at which the pulse fact arrives, and the time span is extended to T. The above shows the Dirac pulse, which behaves like a pure delay. Note that moving T0 to T/2 reduces the frequency resolution (2/T).
There is a causal relationship between these “pre-delay†and the factual time, but there is no causal relationship with the main information arrival time. This allows the filter to compensate for the reflected energy through the opposite "negative time" response.
Therefore, if the point length is 1024 points, the linear phase FIR filter will place the main arrival time at T/2, allowing half of the filter length to provide a pre-arrival time to conjugate the speaker or room-generated back-elevation energy. It also allows the introduction of the required negative group delay to compensate for the all-pass response of the divider.
Since half of the filter length is used for "negative time" correction, the frequency resolution of the filter will be halved. For example, the minimum phase FIR filter frequency resolution of 1024 points is 47.6 Hz. The linear phase FIR filter of the same length has a frequency resolution of 95.2 Hz because half of the length is reserved for phase equalization.
The more points, the better?
This seems to be the case for a minimum phase FIR filter. The problem is that the non-minimum phase filter needs to reserve half the length for phase equalization. This will manifest as a processing delay (often incorrectly referred to as a delay). Unlike the minimum phase FIR filter, as the length of the linear phase FIR filter increases to increase its frequency resolution, its delay will also increase. This is not caused by the speed of the DSP, but by TF = 1.
Now I will call up my reference file, but this time it is a series of cut filters, the frequency of which is the same as the original boost filter (Figure 10). As you learned from the previous discussion, the group delay view (blue line) shows the length of time the filter rings. Note that it is now negative, but this only means that the phase offset produced by this filter is constantly expanding throughout the bandwidth. It does not mean that "time advance" or the response of the filter is non-causal.

Figure 10: A series of cut filters for the equalization reference file. It can be observed that the group delay (right axis) of several octaves of lower frequencies is unavoidably very long.
Unavoidable, the lower the frequency, the longer it takes for the filter to take effect, and the time at the center frequency of the lowest octave (31.5 Hz) will become very long (~40 ms). For live performances and many fixed installation applications, such long processing delays are unacceptable. A 1024-point FIR filter (48 kHz sample rate) is 21 milliseconds in length, which means the processing delay is approximately 10.5 milliseconds.
Increasing the sample rate to 96 kHz does not reduce the processing delay because the number of samples that must be processed is doubled. The fact that it cannot be changed is that the minimum length of 21 milliseconds can only affect 48 Hz, and the fact that the frequency resolution is three times that of 48 Hz, or 150 Hz.
The problem is getting worse
Linear phase FIR filters have another disadvantage. Since "relative time zero" is in the middle of the filter duration, its frequency resolution is half that of the minimum phase FIR filter.
Therefore, if a 1024-point minimum phase FIR filter can affect 150 Hz at the lowest, then a 1024-point linear phase FIR filter can only affect 300 Hz at the lowest.
A frequency of influence to dive to 150 Hz would require a 2048 point filter, meaning that the processing delay would have doubled from 10.7 milliseconds to 21 milliseconds.
For my demo file, an 8196-point FIR filter will be required to smooth the response of the entire passband. The processing delay required is approximately 85 milliseconds.
On the surface, the longer the length of the FIR filter, the better it seems to be to increase the frequency resolution, thus:
1) Affect lower frequencies.
2) Contain more details throughout the bandwidth.
I have shown you that at least for linear phase FIR filters, affecting lower frequencies (more bits) will increase processing latency. This is not due to insufficient processing power, but rather to the correlation of time and frequency. The low frequency lasts for a long time and takes up a lot of space. Digital processing cannot change this situation.
Partial benefit
There are a total of 10 octaves in the audible spectrum, so each octave occupies one tenth of the whole (log scale). Double the filter length will double the processing delay, which only makes the spectrum of your equalization processing one-tenth.
It's like doubling the power of the amplifier just to get a 3dB boost, sometimes at a critical point, and getting very little return, it's not worth it. In the case of a power amplifier, the cost is money, and for a linear phase FIR filter, the cost is a delay. It can be said that the currency of digital processing is time. You can get good results if you can wait long enough.
In most rooms, the lowest two octaves (secondary low frequencies) are below the Schroder Frequency, where room modes have a profound effect on the frequency response of each seat. Even if we pass the linear phase FIR filter, the response of a certain point in the room is very "perfect", and the response in other seats is different. What is the significance of this?
Does that require higher filter accuracy? A 1024-point filter with a frequency separation between data points of approximately 48 Hz. If this is not enough to correct your frequency response, chances are you are trying to correct something that should not be treated at all, such as comb filtering due to room reflections. The more "details" in the frequency response, the more time responses are "position dependent" because these details are caused by reflections from different surfaces.
Moving the test microphone, the response changes a lot. A very accurate FIR filter is only suitable for one point in the "correction" space. This may be useful for echo cancellation of the conferencing system at a particular microphone location, but this does not benefit the entire audience area. Longer FIR filters don't make much sense for field applications.
Is higher sampling rate helpful?
Purely rumors. Unfortunately, this is not the case. Returning to Figure 6, the time interval of the filter point is dt = 1 / SR (sampling rate), multiplied by the number of points (N) to get the length of time (T) of the filter. The frequency resolution (F) is 1/T.
This is a simple relationship, showing that if the sampling rate is doubled, the frequency resolution of the filter will be reduced by half. We made the problem worse! If the sample rate is doubled, the number of samples that need to be processed is multiplied by two, which necessitates doubling the filter length to maintain the same frequency resolution.
Let us examine the opposite situation. Halving the sample rate will increase the frequency resolution of the filter. But to sacrifice high frequency response, it can only be extended to SR/2. The Nyquist-Shannon theorem cannot be denied.
None of this can change the processing delay required for a linear phase FIR filter, which is half the filter duration. A higher (lower) sampling rate does not change the time, frequency or wavelength of the signal.
in conclusion
There is no doubt that we will have longer digital filters in the future as technology evolves. The chip is constantly improving, as is the product using the chip. We may recall that 16-bit/44.1 kHz "CD-level" audio was once almost impossible to achieve. But today many people think that its resolution is very low. FIR filters will also evolve along such trajectories.
But implementing a longer filter also encounters some obstacles, and this has nothing to do with technology. As I have shown in the above article, the main obstacle is the processing delay, which is related to the length of time the filter must affect (see Figure 1).
In the live sound system, we can only tolerate a little delay. This standard is not very accurate, but most people will agree that filtering for more than 20 milliseconds is a relatively long time. This unavoidable processing delay increases the latency of other digital devices in the signal chain, typically by an additional 10 milliseconds. In terms of time, we have to give up linear phase equalization for low frequencies, at least for field applications.
Applying a linear phase FIR filter to high frequencies seems to be a solution for applying a minimum phase FIR filter to low frequencies. This is called a "hybrid phase" filter, which I think will be the future trend. Some people are beginning to think that IIR filters are useless, but it is undeniable that they have the widest bandwidth, the lowest processing delay, and use less system resources than any other digital filter. Please don't take my parametric equalizer module!
The number of points cannot be infinitely unlimited, meaning that we must think about what the focus of the correction is and the reasons behind it. Just like there is only one spoonful of peanut butter left in the jar, we have to make good use of it. How does my equalization affect the entire coverage area of ​​the speaker, not just the "golden position" of the test microphone? If multiple seats are considered, the magical aura of the linear phase FIR filter will quickly fade away.
Using a 1024-point FIR filter is better than using a longer filter. Human cognition sets reasonable limits on the sampling rate and bit depth required for analog-to-digital conversion. Time, frequency, wavelength, and delay also limit the benefits of longer FIR filters. In the audio industry, it's always debatable to make things bigger, and digital filters are no exception. This is not a bad thing, it can be balanced, and it makes people think that it is better to look for a real sound, or the data of the specification sheet.
This in turn explains that “less is moreâ€.
Author: Pat Brown translation: Exchanging International please indicate the source