Digital signature technology in hash function

The digital signature technology mentioned in the article is the most important tool we use to ensure identity identity in cryptography. Identity identity means how to prove that a certain message was sent by "I" that others cannot forge and I cannot deny it. Although digital signature technology also uses paired key pairs, it is different from what we call public key cryptography. (2) This article can be regarded as a tutorial or template for thinking about cryptography tools. If you can read it patiently, you will understand what cryptography is all about and how we think in cryptography.

Looking back on the past few years, I have been fortunate enough to experience two conflicting but fascinating changes in the times. The first trend change is that the cryptography that experts and scholars spent 40 years designing finally came in handy; from information encryption, telephone security, to encrypted digital currency, we can find examples of using cryptography in every aspect of our lives.

The second trend is that all cryptographers are ready to meet the above beautiful disillusionment.

Before the text begins, I must reiterate that what this article is about is not the so-called quantum computing apocalypse (doomsday prophecy), nor is it about the success of cryptography in the 21st century. What we are going to talk about is another undecided thing-one of the simplest (and coolest) techniques in the history of cryptography: signatures based on hash functions.

In the late 1970s, Leslie Lamport invented a signature based on a hash function (Hash Function, also known as a hash function), which was further improved by Ralph Merkle and others. For many years, this was regarded as an interesting "dead water" in the field of cryptography, because in addition to the correspondingly lengthy (compared to other complex schemes) signatures, signatures based on hash functions seemed to have no effect. However, in recent years, this technology seems to show signs of recovery. This is largely due to its characteristics-unlike other signatures based on RSA or discrete logarithm assumptions, hash function signatures are considered to be resistant to quantum computing attacks (such as Shor's algorithm).

First, let's make some background introductions.

Background: Hash function and signature method

Before officially introducing the hash function signature, you must first know what the hash function is in cryptography. The hash function can accept a string of characters (of any length) as input, and after "digesting", it produces a fixed-length output. Common cryptographic hash operations, such as SHA2, SHA3, or Blake2, will produce an output with a length between 256 and 512 bits.

A function H(.) To be called a "cryptographic" hash function, it must meet some security requirements. There are many requirements, but we mainly focus on the following three aspects:

Pre-image resistance (or "unidirectional"): Given the output Y=H(X), it is "extremely time-consuming" to find the corresponding input X such that H(X)=Y work. (Of course there are many exceptions here, but the best part is that no matter what distribution X belongs to, the time cost of finding X is the same as a brute force search.)

Anti-subprime attack: This is slightly different from the former. Given an input X, it is very difficult for an attacker to find another X'such that H(X)=H(X').

Anti-collision: It is difficult to find two inputs X1, X2 such that H(X1)=H(X2). It should be noted that the conditions of this hypothesis are more stringent than the anti-secondary preimage attack. Because the attacker can look for any two inputs from the endless choices.

We believe that all the hash function examples mentioned in this article can provide all the features mentioned above. In other words, there is no feasible (or even conceptual) way to crack it. Of course, this situation will change. If a cracking method is found, of course we will immediately disable the hash function (special cases of quantum computing attacks will be discussed later).

Our goal is to use a hash function to construct a digital signature scheme, so a brief review of the term digital signature can be of great help.

The digital signature method originated from the use of public keys. The user (signer) generates a pair of keys: a public key and a private key. The user keeps the private key by himself, and can use the private key to "sign" any message, thereby generating the corresponding digital signature. Anyone who holds the public key can verify the correctness of the message and the relevant signature.

From a security point of view, we hope that the signature is unforgeable, or "there is unforgeability." This means that an attacker (a person without control of the private key) cannot forge your signature on a certain message.

Lamport one-time signature

In 1979, a mathematician named Leslie Lamport invented the world's first signature based on a hash function. Lamport found that as long as a simple hash function or one-way function is used, a very powerful digital signature method can be constructed.

The powerful premise is that the user only needs to do a signature action to ensure safety! A more detailed explanation will be given later.

For a better discussion, we assume the following conditions: a hash function that can accept 256-bit input and produce 256-bit output; the SHA256 hash function is an excellent demonstration tool; we also need a random input method.

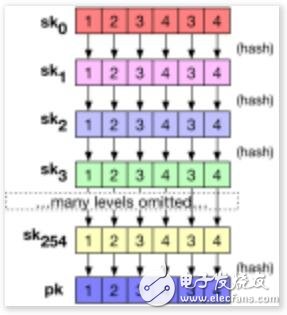
Suppose our goal is to sign a 256-bit message. To get the key we need, we first need to generate a random 512 bit string, each bit string length is 256 bits. For ease of understanding, we have listed these strings as two separate tables, and referred to them with symbols:

sk0= sk10, sk20,. .., sk2560

sk1= sk11, sk21,. .., sk2561

We use a list (sk~0~, sk~1~) to indicate the keys used for signing. Next, in order to generate the public key, we hash the random bit string through H(.) to obtain the public key as follows:

pk0= H(sk10), H(sk20),. .., H (sk2560)

pk1= H(sk11), H(sk21),. .., H (sk2561)

Now we can publish the public key (pk~0~, pk~1~) to everyone. For example, we can send the public key to a friend, embed it in a certificate, or publish it on Keybase.

Then we use the key to sign the 256-bit message M. First, we have to reproduce the message M as an independent 256-bit (Bit, also known as "bit"):

M1, M2,. .., M256 ∈ {0, 1}

The rest of the signature algorithm is very simple. We take out the string from one of the keys in the key list one by one from the 1st to the 256th bits of the message M. The selected key depends on the value of each bit of the message we want to sign.

Specifically, for i = [1,256], if the i-th message bit Mi = 0, we will select the i-th character (ski0) from the sk0 table as part of our signature; if the i-th The message bit Mi = 1 of the bit, we perform the aforementioned process from the sk1 table (that is, if we want to sign the 3rd bit in the message M, and the bit value is 0, then the third bit in sk0 is used, sk03, as part of our signature). After completing this operation for each message bit, we will concatenate the selected strings to get the signature.

The process is as shown in the figure, because part of the process is simplified, the key and message length are only 8 bits (bits). It should be noted that each color block represents a different random 256-bit string.

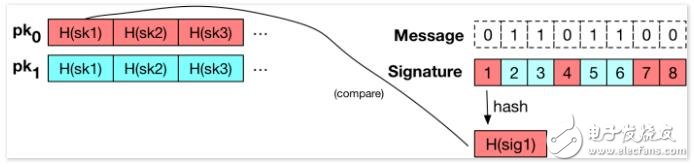
When a user (who already knows the public key (pk0, pk1)) receives the message M and the signature, she can easily verify the signature. We denote the i-th component in the signature with si, and the user can check the corresponding message Mi and calculate the hash value H(si). If Mi = 0, the hash value must match the element in the public key pk0; if Mi = 1, the hash value must match the element in the public key pk1.

If each element in the signature is hashed and the corresponding correct part of the public key can be found, we will say that the signature is valid. The following is an illustration of the verification process. There is at least one signature element in the signature:

If you start to think Lamport’s plan is a bit crazy, you are both right and wrong.

First, discuss the shortcomings of this digital signature method. We will find that the signature and key of the Lamport method are too large, about thousands of bits. What's worse, this method has serious security limitations: each key can only be used to sign one message, so the Lamport method is used as an example here as a "one-time signature".

Why does this security limitation exist? Recall that the Lamport signature indicates one of the two possible keys on each message bit. If only one message needs to be signed, this signature method is completely fine. However, if I sign two messages with different bit values ​​at each corresponding position i, and then send them together with the key, this may cause big problems!

Assuming that the attacker obtains two valid signatures from different messages, she can launch a "mix and match" attack, successfully forging and signing the third piece of information that I have never signed. The following diagram illustrates the attack process:

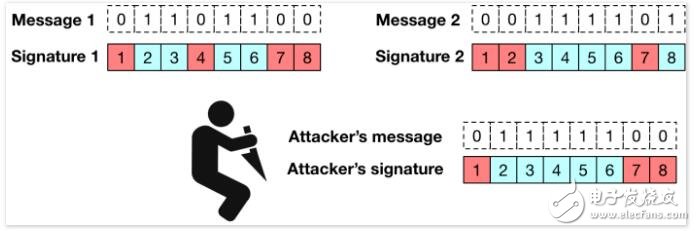
The severity of this problem depends on how different the messages you signed and how many messages were intercepted by the attacker. But in general, this is certainly not a good thing.

Let us summarize the Lamport signature method; it is simple and fast, but it has many shortcomings in practical applications. Maybe we can do a little optimization?

From one-time signature to multiple signatures: Merkle's tree-based signature

The Lamport signature method is a good start, but the inability to sign multiple pieces of information with a single key is its biggest drawback. Ralph Merkle, a student of MarTIn Hellman, got a lot of inspiration from this, and he quickly thought of a clever solution.

Although we are not going to explain the steps of Merkel's method here, let's try to clarify Ralph's thoughts.

Our goal now is to sign N messages using Lamport's signature method. The most intuitive method is to use the original Lamport method to generate N different key pairs, and then associate all public keys to form a huge mega-key. (Mega-key is a term that I have compiled now.)

If the signer continues to hold such a set of keys, she can sign N different messages, which is strictly a Lamport key. It seems that this solves the problem of key reuse. The verifier also has the corresponding public key to be able to verify all received messages. No Lamport key is used twice.

Obviously, this method is bad because the time cost is too high.

Specifically, in the above-mentioned naive method, in order to achieve the required number of signatures, the signer must distribute a public key that is several times larger than the ordinary Lamport public key (the signer must continue to hold the same huge private key) . People are likely to be dissatisfied with this result, and they will also reflect on whether there is a way to avoid this negative effect. Next, let us enter the Merkle method.

The Merkle method hopes to find a way to sign multiple different messages while avoiding a linear surge in the cost of public keys. The Merkle method is implemented as follows:

1. First, generate N independent Lamport keys, we use (PK1, SK1),. .., (PKN, SKN) means it.

2. Next, put each public key into the Merkle hash tree (see the figure below), and calculate the root node hash value. This root node will become the "master public key" in the Merkle signature method.

3. The signer declares all Lamport keys (public key and private key) for signing.

For more description of Merkle tree, please click here. Roughly speaking, the Merkle method provides a way to collect different values ​​and use a "root" hash (the hash function used in the example, the length is 256 bits) to represent the collected value. Given this root hash, you can simply "prove" that an element exists in the given hash tree. And the size of this proof is logarithmically related to the number of leaf nodes.

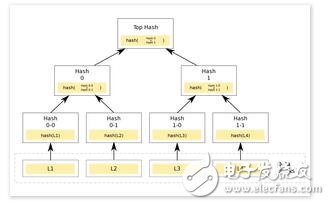
-Merkle tree, an explanation from Wikipedia. The Lamport public key is put into the leaf node, and then the root node becomes the master public key. -

When signing, the signer directly selects the public key from the Merkle tree and signs with the corresponding Lamport key. Then she connects the signature result to the Lamport public key and attaches the "Merkle certificate." Merkle root can be used to prove that the Merkle tree contains the selected public key (that is, the public key used in the entire method). Finally, the signer sends the entire set as a message signature.

(The verifier can perform verification by decompressing the “signature” directly into Lamport signature, Lamport public key, and Merkle proof. The verifier can rely on the Lamport public key to verify the Lamport signature, and use Merkle to prove that the public key is indeed Exists in the Merkle tree. As long as these three conditions are met, the verifier can be sure that the signature is valid.)

The disadvantage of this method is that it increases the size of the "signature" more than twice. However, now the main public key of the Merkle method is just a string of simple hash values, making this method more concise than the original Lamport method mentioned above.

Finally, there is an optimization part. The pseudo-random number generator with cryptographic strength can output and generate various keys while "compressing" the key data itself. This allows the original huge bits (obviously random) to be converted into short "seeds."

That's awesome!

Make signatures and keys more efficient

The Merkle method turns a one-time signature into an N-time signature. The construction of this method still needs to be based on some one-time signature methods, such as the Lamport method; but unfortunately, the (bandwidth) cost of the Lamport method is still relatively high.

There are two main ways to reduce these costs. The first is also proposed by Merkle; in order to better explain many powerful signature methods, we give priority to this technology.

Recall the Lamport method. To sign a 256-bit message, we need a vector containing 512 independent key (and public key) bit strings. The signature itself is a collection of 256 key bit strings. (These numbers will be activated by the message bits that need to be signed. The bits can be "0" or "1", so the appropriate key element needs to be extracted from two different key tables.)

This leads to new thinking: what if we don't sign all the message bits?

In more detail, in the Lamport method, we sign each bit of a message by outputting the key bit string-no matter what its value is. What if we don't sign the 0 and 1 bits of a message at the same time, but only sign the 1 bit? Doing so can halve the size of the public and private keys, because we can completely discard the entire sk0 column.

Now we only have the key sk1, which is a single bit string. .., sk256, for each bit Mi = 1 of the message we will output a string ski; for each bit Mi = 0 of the message we will output. ... .. None (because many messages will contain a lot of 0 bits, this can reduce the size of the signature, these 0 bits will no longer incur any cost).

The obvious flaw of this method is that it is extremely insecure, so please don't do it!

For example, suppose an attacker observes a signed message with the beginning of the message "1111...". Now the attacker wants to edit the message to "0000..." without destroying the signature, and only needs to delete a few components of this signature! In short, although it is difficult to "flip" 0 bits into 1 bits, it is very simple to change 1 to 0 on the contrary.

Now there is a solution, and it is very clever.

Let's take a look. Although it is unavoidable that the attacker changes the 1 in the message to 0, we can find these changes. Just attach a simple "checksum" to the message, and then sign the message and the checksum together. For the signature verifier, she must verify the two values ​​of the entire signature, and also needs to make sure that the received checksum is correct.

The checksum we use is very small: it consists of a simple binary integer, which represents all 0 bits in the original message.

If an attacker tries to modify the content (or checksum) of the message so that part of the 1 bit becomes 0 bit, there is no way to stop her. But this kind of attack will increase the number of 0 bits in the message, which will invalidate the checksum, and the verifier will therefore reject the signature.

Of course, a witty attacker may also try to obfuscate the checksum (the checksum is also signed with the message) and increase the integer value of the checksum to match the number of bits she tampered with. However, the most important thing is that because the checksum is a binary integer, if the value of the checksum is to be increased, the attacker is bound to convert some 0 bits into 1 bits. Because the checksum is also signed, this signature method prevents this conversion from the source (replacing 0 to 1), so the attacker cannot succeed.

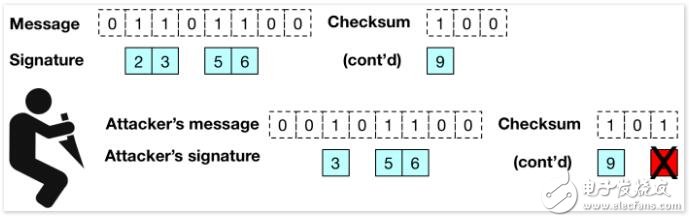
(If you continue to record, it will indeed increase the size of the signed "message". In our example, the checksum of a 256-bit message requires an additional 8 bits and the corresponding signature cost. However, If the message contains many 0 bits, this is still very effective for reducing the size of the signature.)

Transparent LED Display

P3.91-7.82 Transparent LED Display

Features:

*Ventilated light
*Free air conditioning heat saving energy
*Environmental protection- it uses only a third of the power of a conventional Led screen
* Convenient installation High compatibility

Application:

Movie theaters, clubs, stages.

Transparent LED Display,Transparent Led Display,Transparent Poster Led Display,Led Screen Panel

Guangzhou Chengwen Photoelectric Technology co.,ltd , https://www.cwledpanel.com